
Finally, note that our new vectors, or axes, are uncorrelated. Also, note that the spatial relationships of the points are unchanged this process has merely rotated the data. In this new reference frame, note that variance is greater along axis 1 than it is on axis 2.
Once we have made these vectors, we could find the coordinates of every data point relative to these two perpendicular vectors and re-plot the data, as shown here (both of these figures are from Swan and Sandilands, 1995). Both vectors are constrained to pass through the centroid of the data. We could pass one vector through the long axis of the cloud of points, with a second vector at right angles to the first. The two are highly correlated with one another.

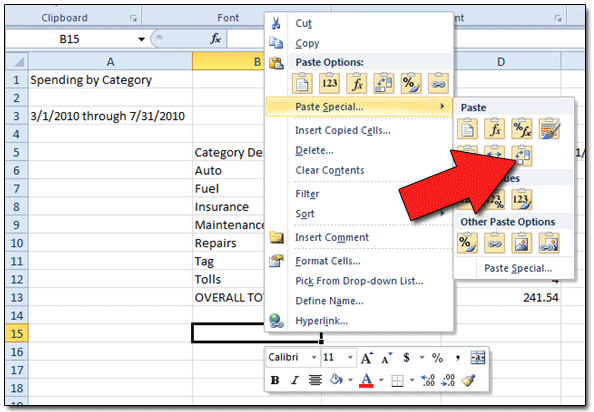
Suppose we had measured two variables (length and width) and plotted them as shown below. Principal Components Analysis Introduction


 0 kommentar(er)
0 kommentar(er)
